単なる長方形ではなく、複雑な形をした領域の「塗りつぶし」を行うアルゴリズムを考えてみます。ここで考える領域とは、「指定された点と繋がっている同じ色の場所の集合」であり、その領域内に指定された色を置いて行くアルゴリズムを検討してみましょう。
最も単純に考えれば、指定された点を出発点に「周囲に出発点と同じ色のドットがあれば色を付ける」処理を繰り返せばよい事になります。つまり、自分の周囲を見て色を付ける処理を再帰的に行うアルゴリズムです。
最初はそもそもJava で再帰が上手く働くか不安だったのですが、小さい領域ではうまく動くようです。最も、大きくなるとどうなるか不安は残りますが。
まあ、大きな領域で実行する時には改めて最適化するとして、今回はとりあえず32*32の配列を対象に「塗りつぶし」処理をやってみましょう。これくらいならどんな処理系でも大丈夫.....だと思います。
まず、配列の各要素を0が白で1が黒、2を赤に対応させます。つまり、画面にこの配列の様子を表示する時には0なら白、1なら黒、2なら赤という風に表示するわけです。配列の大きさは32*32ですが、隅の1ドットは3(青)で囲っておき、塗りつぶしの出発点は(16、16)という事にしました。
自分の周囲を見て出発点と同じ色なら塗りつぶす処理をする、というのは上下左右を見て出発点と同じ要素があれば、それを指定された数値に書き換える、というアルゴリズムになります。
今回配列の要素は0ー3なので、塗りつぶし処理の途中ではではー1を置いておいて、後からまとめてー1を指定した数値に変換するようにしましょう。後は、この処理を再帰的に行えば、つまり
private void fill(int x,int y) { /* 塗りつぶし */
dot[x][y]=-1; /* ー1を置く */
if (dot[x][y-1]==cl) /* 上に自分と同じ色があるか */
fill(x,y-1); /* あればその座標で再帰呼び出し */
if (dot[x+1][y]==cl) /* 右 */
fill(x+1,y);
if (dot[x][y+1]==cl) /* 下 */
fill(x,y+1);
if (dot[x-1][y]==cl) /* 左 */
fill(x-1,y);
}という関数を初めにfill(16,16)と呼び出せば良い事になります(cl が最初(16、16)にあった数値)。この関数を一度呼び出せば、連続する領域内を再帰的に走査して、すべて塗り終えた(領域内に最初の色がなくなった)段階で関数は終了するからです。このアルゴリズムの処理を、図で考えてみましょう。
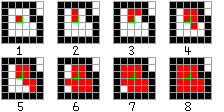
まず、(1)では緑色で示した出発点(白だったとします)が塗りつぶされ、ー1(赤で表示)になります。次に、その上を見ると「出発点と同じ色」(if (dot[x][y-1]==cl))という条件を満たすので、そこの座標を引数に自分自身を再度呼びました。すると、その座標も塗りつぶされ(2)、if 文の条件が調べられます。
今度は上を見ると出発点とは違う黒なので、偽となり次に調べるのは右です。右を見るとそこは出発点と同じ白なので、またその座標を引数にfillを呼び出すのが(3)。(7)になると周囲はすべて塗りつぶされていますので、関数は戻りはじめます。そして、
2つ戻って下を見るとまだ塗りつぶされていない点を発見。そこで最後の塗りつぶしが行われました(8)。
と、このように次々に領域が走査され塗りつぶされるわけです。こうして領域がすべて塗りつぶされると関数は終了し、呼び出し元へ順次帰っていきます(これが再帰の終了条件)。帰って行く過程ではすでに領域内のすべての点が出発点とは異なるー1になっているので、関数内のif 文はすべて偽となり再び自分自身を呼び出す事はあり得ません。
最後に、配列内のー1の要素をすべて塗りつぶしの数値で置き換えれば完成。注意すべきは、走査の段階で配列の要素を塗りつぶす時には、元の配列に絶対にあり得ない数値を使う必要がある、という点です。そうしないと、出発点の領域(ある程度の大きさを持つ場合)と同じ色で塗りつぶそうとした時に、永遠にif 文が真になるため無限に再帰が続いてしまいます(実際にはエラーになるか暴走する)。
プログラムでは、32*32のマス(2次元配列 dot[x][y])の各要素を表示してあります。グラフ内の点をクリック・ドラッグすると値を変えられるので、適当な領域を作ったらG o ボタンで塗りつぶしてみましょう。
なお、外側を3で囲ってあるのは、溢れ出すのを防止するためです。